本篇随笔主要记录了我学习红黑树的过程,用于个人备忘,有不对的地方,请指出。
红黑树简介
红黑树主要是对内存中比较小规模的数据进行索引,内存中索引比较常用的数据结构是BST,外存中是B树及B+树。
内存中索引比较常用的数据结构是BST,其存在的问题是树可能非常不平衡。红黑树就是为了平衡BST而存在的数据结构,其通过规定的颜色限制达到红黑树的平衡,这个平衡并没有达到AVL树中的严格平衡,但红黑树相比于AVL树有以下优势:
如果插入一个node引起了树的不平衡,AVL和RB-Tree都是最多只需要2次旋转操作,即两者都是O(1);但是在删除node引起树的不平衡时,最坏情况下,AVL需要维护从被删node到root这条路径上所有node的平衡性,因此需要旋转的量级O(logN),而RB-Tree最多只需3次旋转,只需要O(1)的复杂度。
红黑树:平衡的 扩充 二叉搜索树。在二叉搜索树的基础上,红黑树增加的五个特征如下:
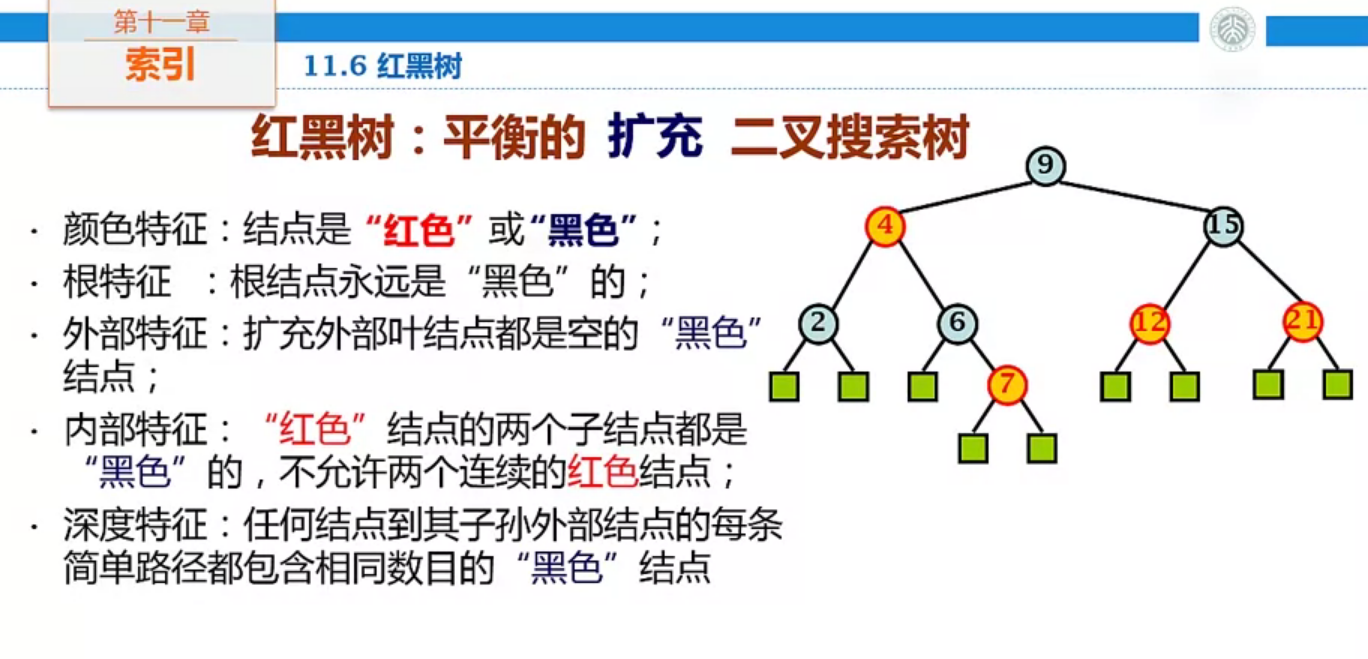
- 颜色特征:节点是红色或黑色
- 根特征:根节点永远是黑色的
- 外部特征:扩充外部叶节点都是空的黑色节点
- 内部特征:红色节点的两个子节点都是黑色的,不允许两个连续的红色节点
- 深度特征:任何节点到其子孙外部节点的每条简单路径都包含相同数目的黑色节点
节点X的阶:即从该节点(不包括该节点本身)开始到外部节点的黑色节点数量。外部节点的阶是0,根的阶称为该树的阶。
阶为K的红黑树即代指根节点的阶为K。
- 红黑树是满二叉树,空叶节点也看做节点。
- 阶为K的红黑树路径长度最短是K(全为黑色节点),最长是2K(路径上红黑节点相间)
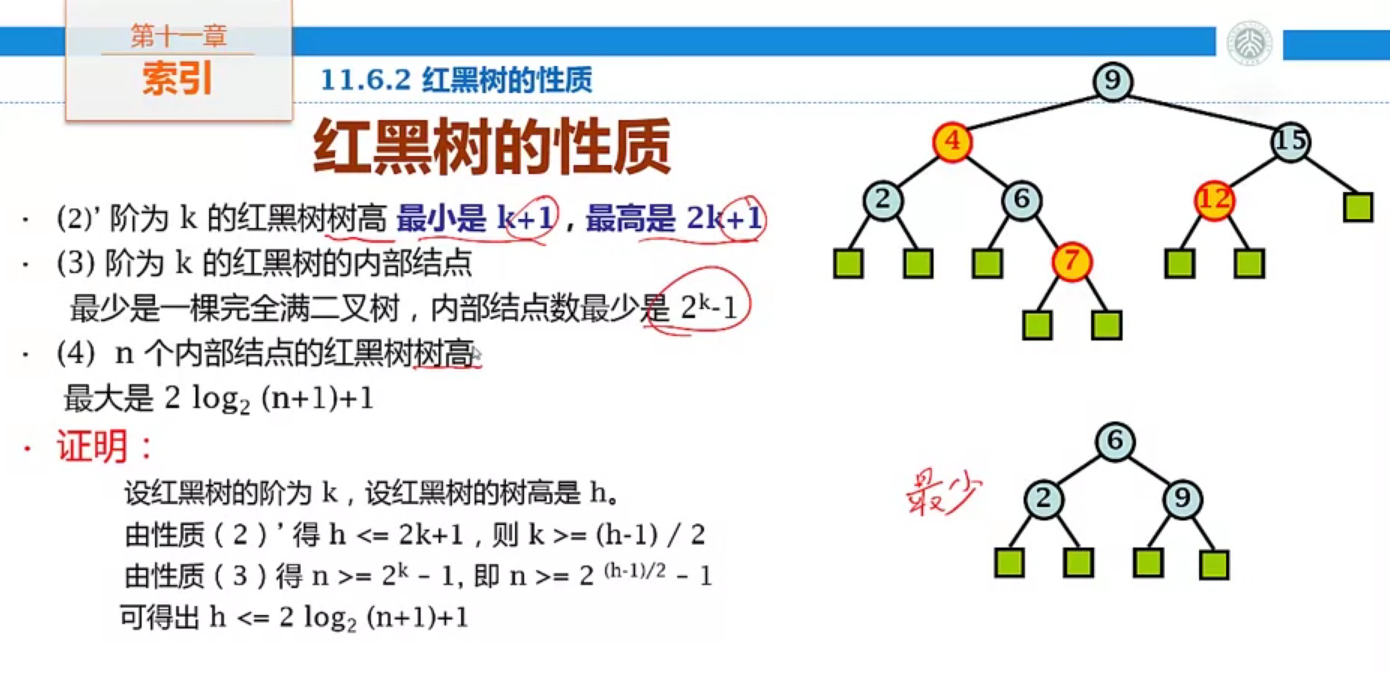
- 阶为K的红黑树树高最小是K+1,最高是2K+1。
- 阶为K的红黑树的内部节点最少是一棵完全满二叉树,内部节点数(不包含外部空节点)最少(完全没有红节点)是2^k-1
- n个内部结点的红黑树树高最大是2*log(n+1) + 1, log以2为底。证明如下:
红黑树插入算法
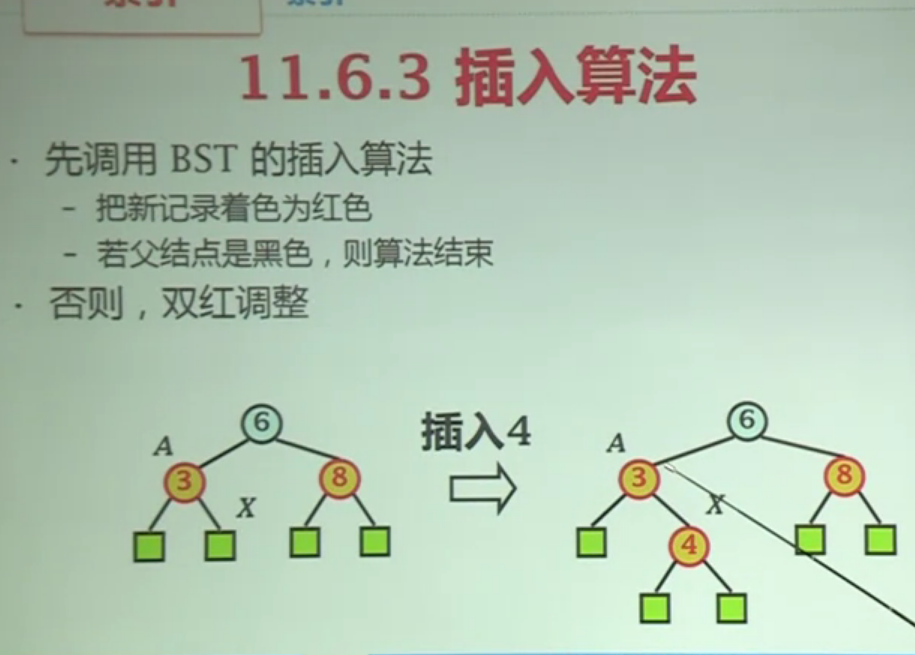
新插入的节点默认为红色,插入之后可能出现红红冲突,下面是调整过程介绍:
- 情况1:新增节点X的叔父节点是黑色,下图中节点C即为节点X的叔父节点
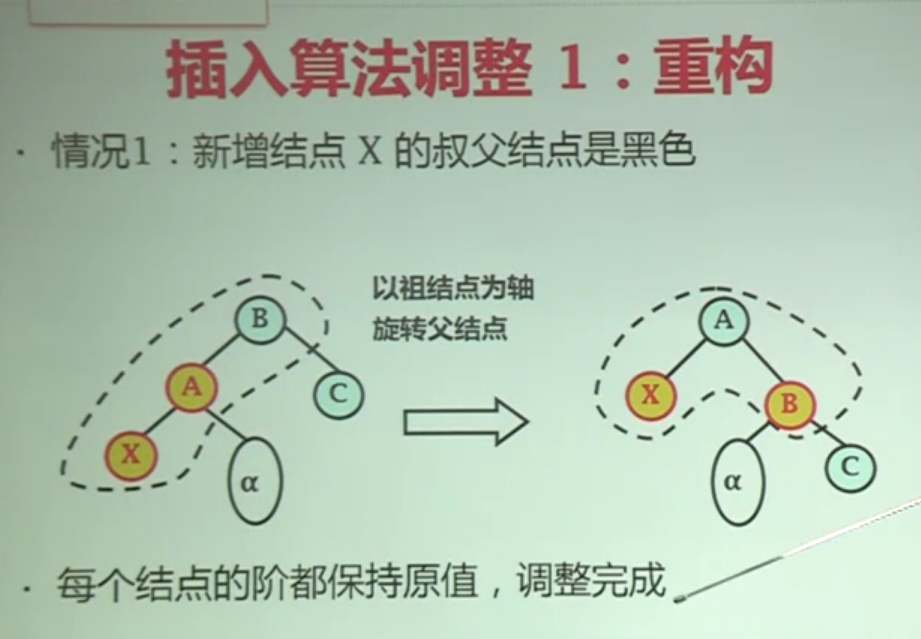
对于红黑树插入时叔父节点为黑色的结构调整其实共四种情况如下图:
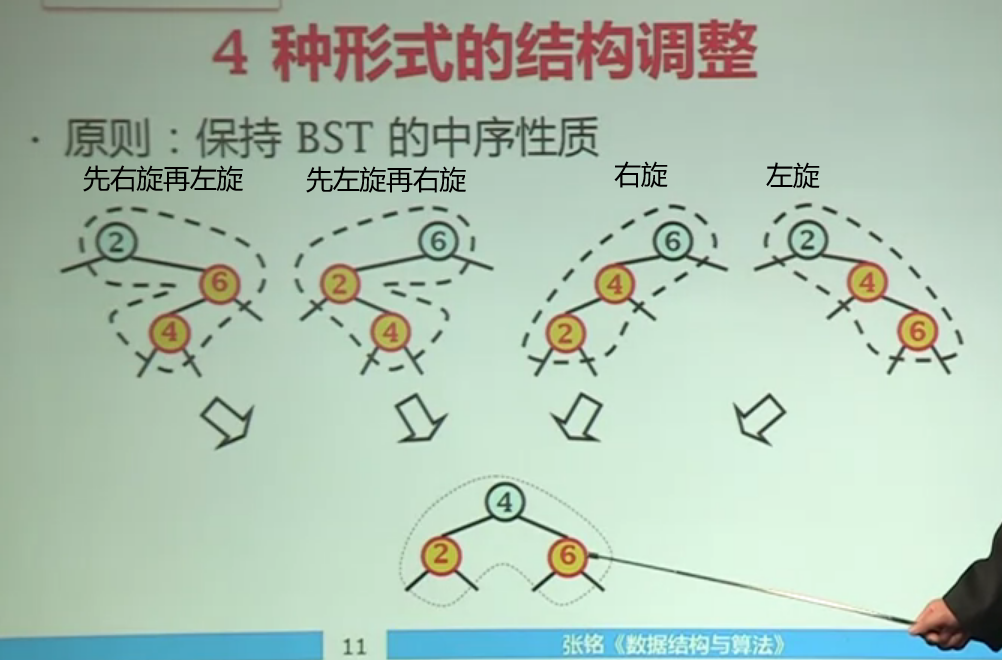
对红黑树插入后的调整的原则是要保持BST的中序下元素有序的性质。
- 情况2:新增节点X的叔父节点也是红色
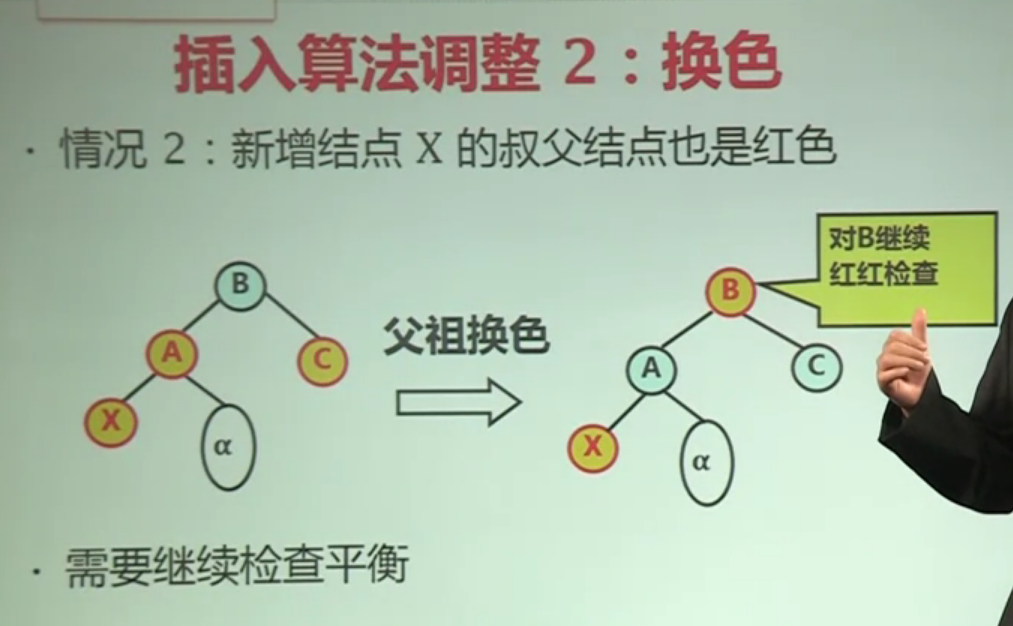
下图是插入4时发生红红冲突的调整示例:
- 4、5冲突,并且4的叔父节点8是红色,首先进行父祖换色,按上面介绍的情况2来调整
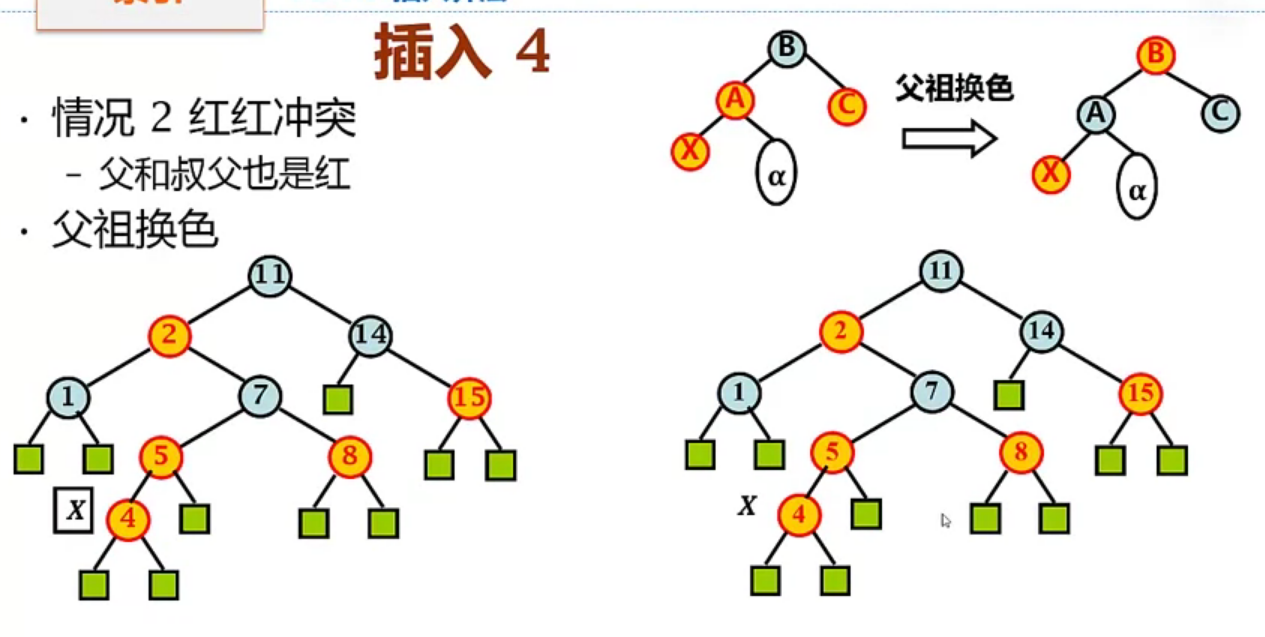
- 换色后7变为红色,与2红红冲突,但7的叔父节点为黑色,所以按照上面介绍的情况1来旋转调整
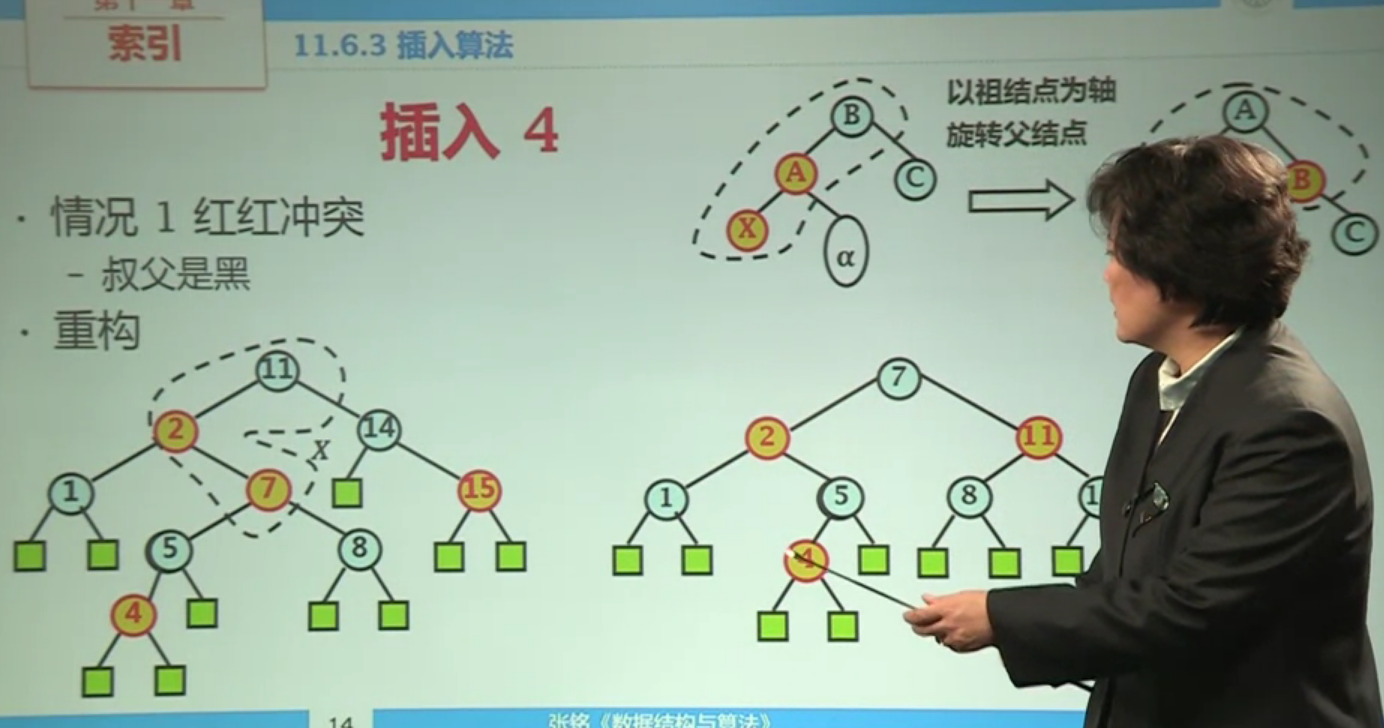
经过上述两步调整过程之后,插入操作完成。
红黑树插入后的调整过程中,情况2换色的时间复杂度为O(logn),简化为情况1之后最多需要进行两次旋转(先左旋再右旋或者反过来)。
红黑树删除算法
实际是基于BST的删除算法进行的,删除之后将被破坏的红黑性质恢复:
- 情况1:如果被删除节点左右子节点均为空(即外部节点),则直接将此节点删除;如果被删除节点有一个子节点为空,另一个不为空,则将此节点删除之后令不为空的子节点挂接到当前节点所在的位置
- 情况2:如果它的左右子节点均不为空,则需要找到其直接中序后继节点(右子树里面的最小节点)的值替代这个待删除的节点(只交换值,不交换颜色),之后删掉此直接中序后继节点,由于此直接中序后继节点至少有一个子节点为空,删除此节点的情况一定属于情况1。
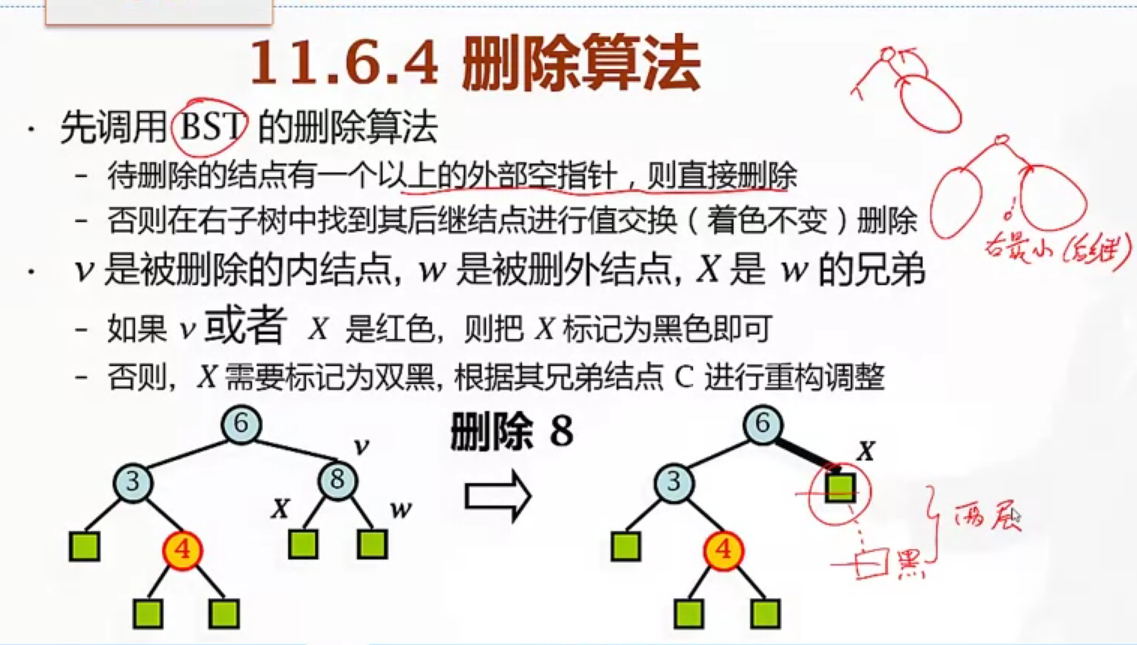
删除节点之后,我们就需要进行颜色的恢复: 如图8所示,V是被删除的内节点,W是被删除的外节点,X是W的兄弟(X可能为外节点也可能为内节点,因为被删除的节点V至多含有一个内节点)
- 如果v或者x是红色,则把x挂接到v的位置后将x标记为黑色即可,不需要再进行多余颜色调整操作。
- 否则,x就需要被标记为具有双重黑色,需要根据其挂接后的兄弟节点C(图8中的节点3)进行重构调整
对于删除之后,X被挂接到被删除节点所在位置,且X被标记为双黑,颜色情况调整有以下几类:

下面是图9中3种情况的详细讨论:
1.情况1(a)重构:侄子为红节点,8字型(x兄弟节点c的右孩子为红色,左孩子任意颜色,属于这种情况)

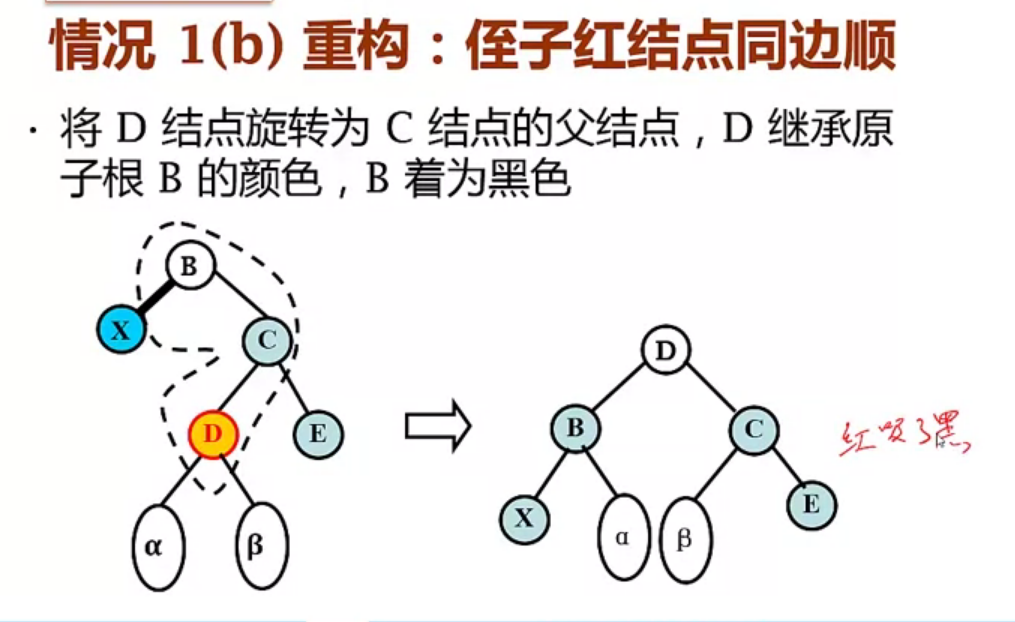
情况1(b)重构:侄子为红节点,同边顺(x兄弟节点c的左孩子为红色,右孩子为黑色,属于这种情况)
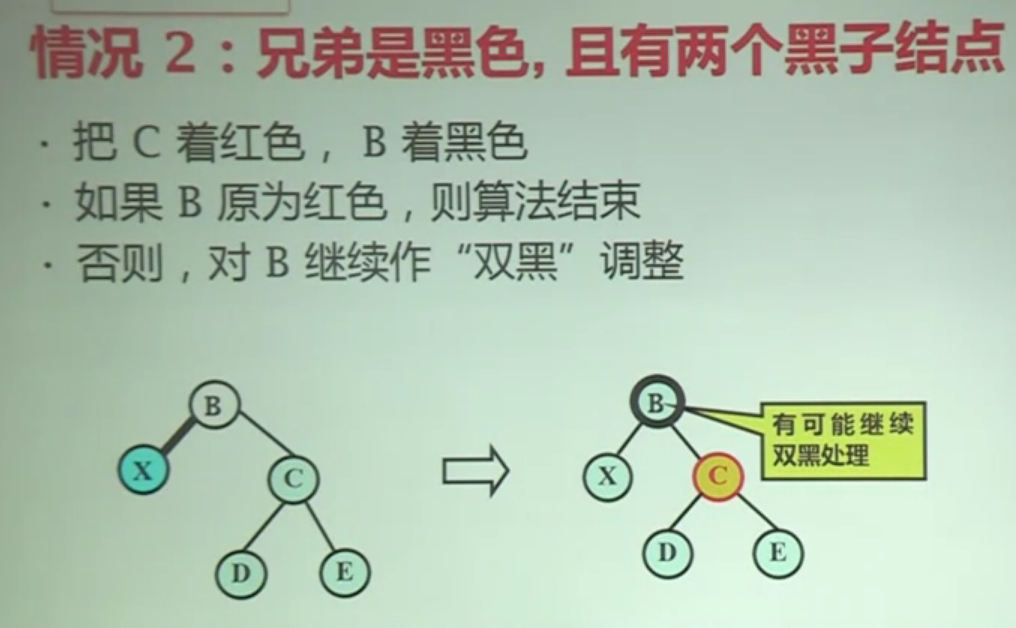
2.兄弟是黑色,且有两个黑子节点
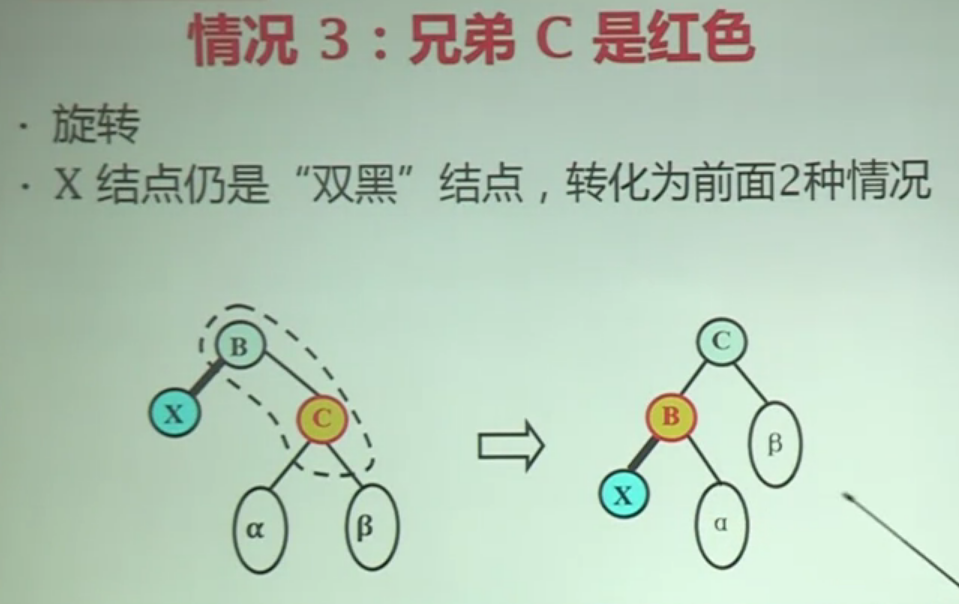
3.兄弟C是红色
具体删除示例:
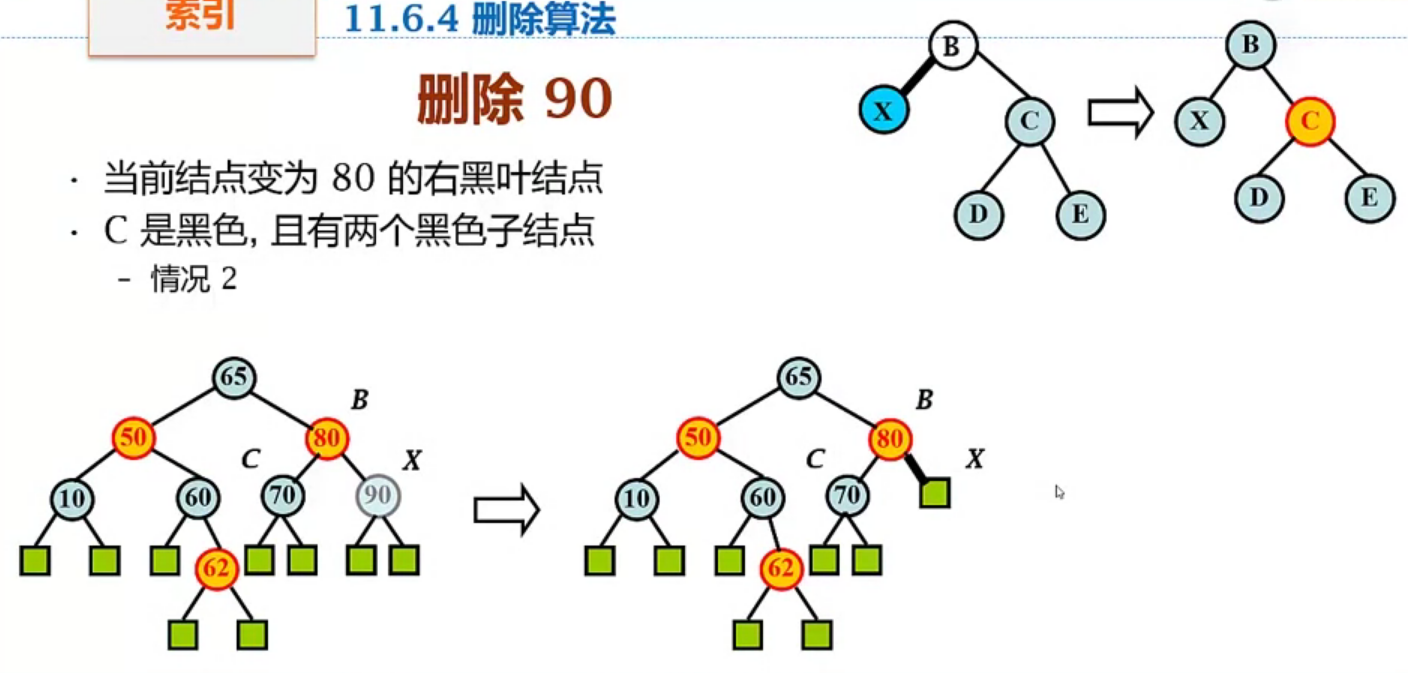
上图中待删除节点90左右子节点均为外部节点,可以直接将此节点删除;删除之后X被标记为双黑,此时即需要进行颜色的调整;X的兄弟节点C属于黑色节点,且有两个黑子节点,属于上述讨论的情况2,由于父节点B为红色,将B、C换色之后本次删除操作就完成了。
删除90后情况如下:
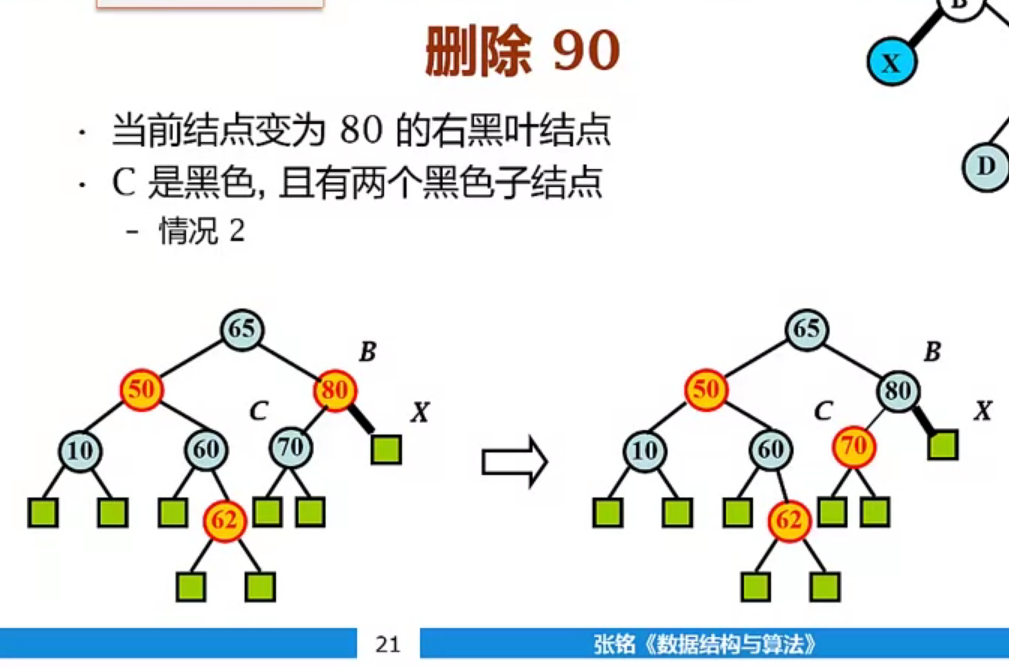
接下来删除70,由于70原来为红色,删除之后直接将X挂接到70所在的位置并标记为黑色即可。
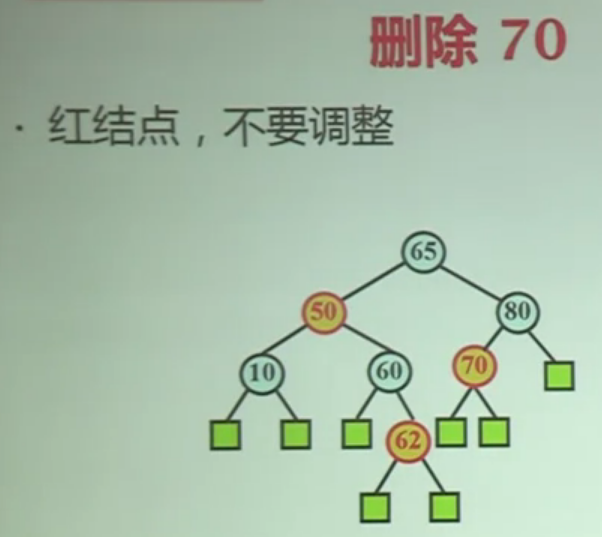
删除70后情况如下:
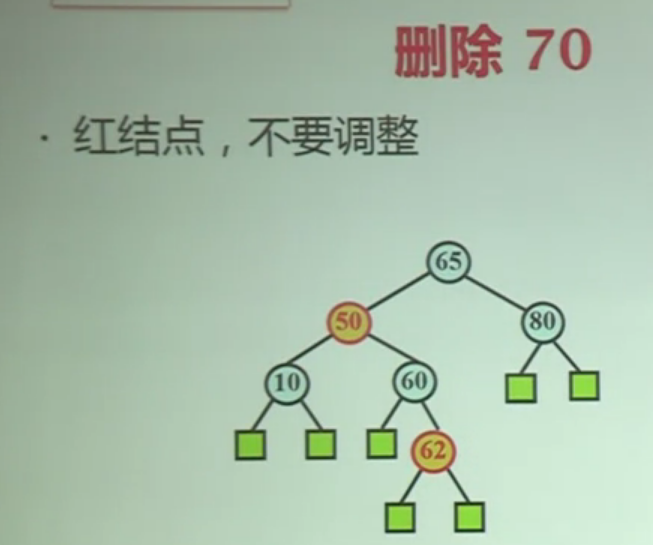
接下来删除节点80,删除之后X被标记为双黑,X的兄弟节点为红色,属于上述情况3,先将其旋转,旋转之后X的兄弟节点变为了60,且侄子节点为红节点同边顺,简化为了情况1(b):
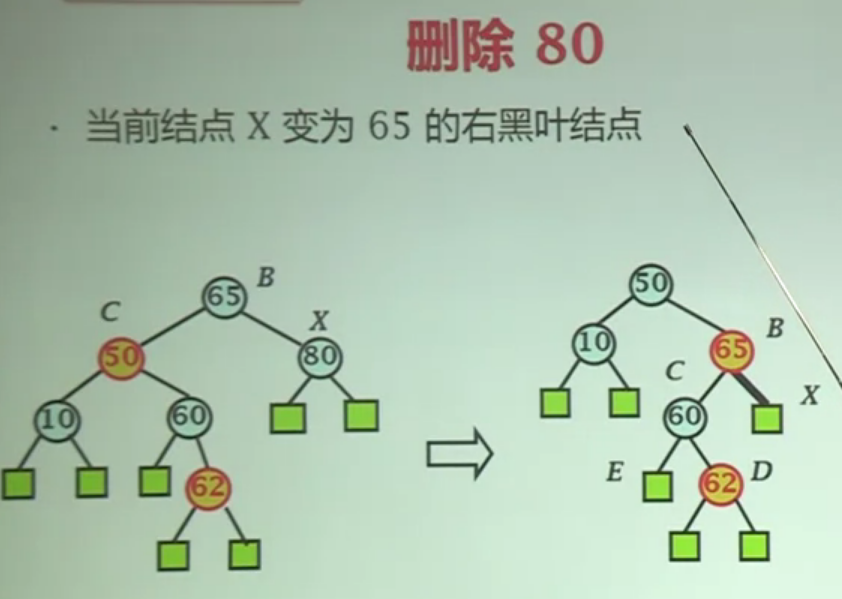
按情况1b进行重构之后完成节点80的删除操作:
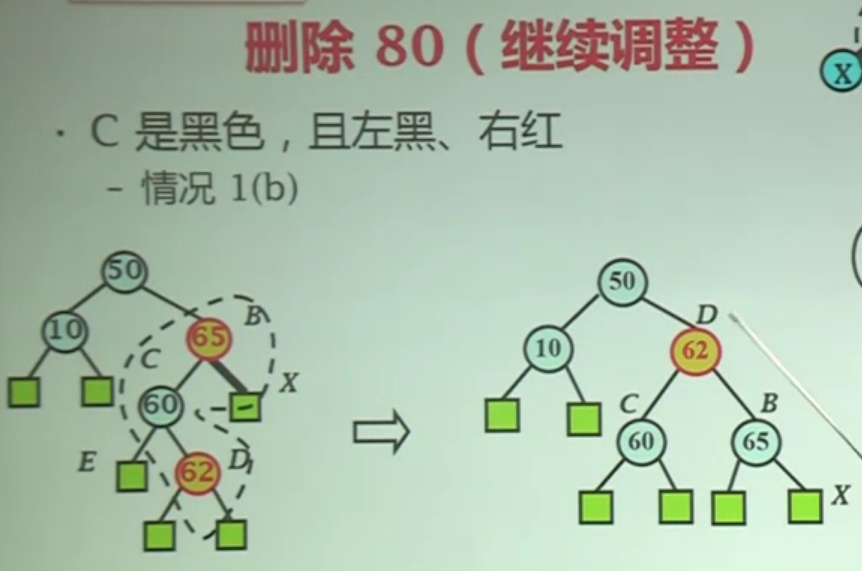
对于红黑树的删除操作,删除一个节点之后最多进行3次旋转操作就能使树满足要求,下面是一个删除后进行3次旋转操作的示例:
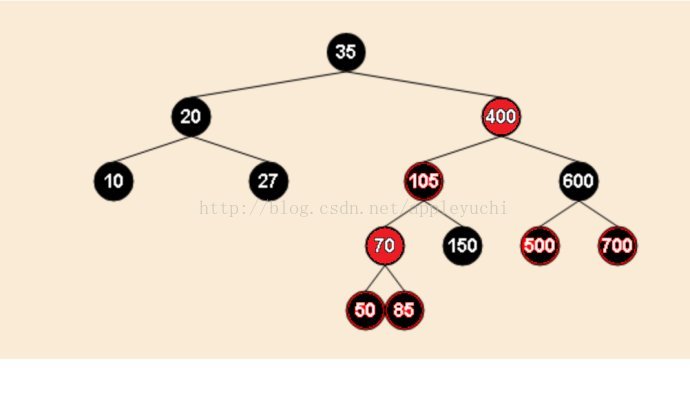
要删除的节点是图20中的节点10,由于节点10及其父亲均为黑色,删除后节点10所在位置标记为双黑外部节点,接下来进行双黑的调整,由于其兄弟节点为27,且有两个黑色外部子节点,属于上述情况2,按情况2要求进行操作后节点27变为红色,节点20变为双黑节点:
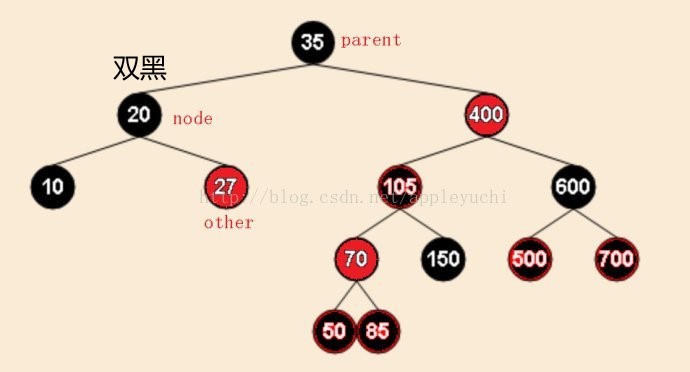
接下来要化解掉节点20的双黑情况,节点20的兄弟节点为红色,符合情况3,需要进行旋转,旋转之后节点20仍为双黑,如下图:
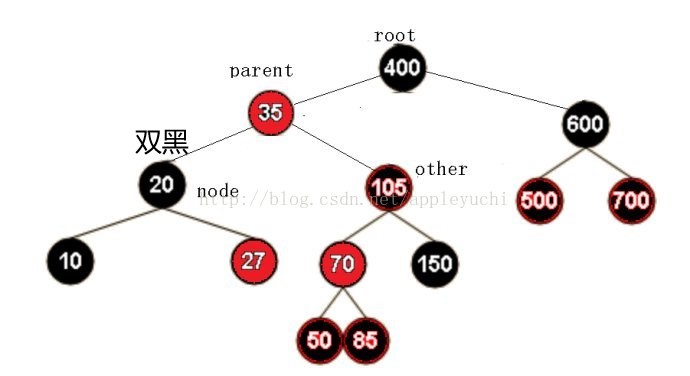
接下来还要化解掉节点20的双黑情况,符合情况1b,需要先右旋再左旋,右旋后如下:
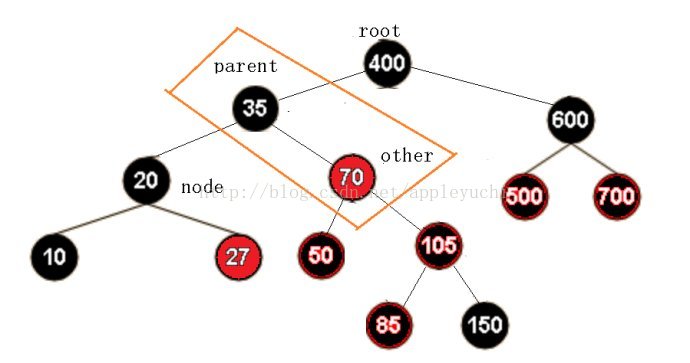
再进行左旋:
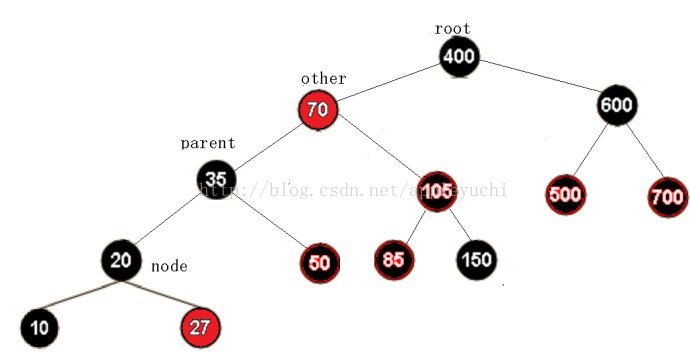
最终删除节点10:
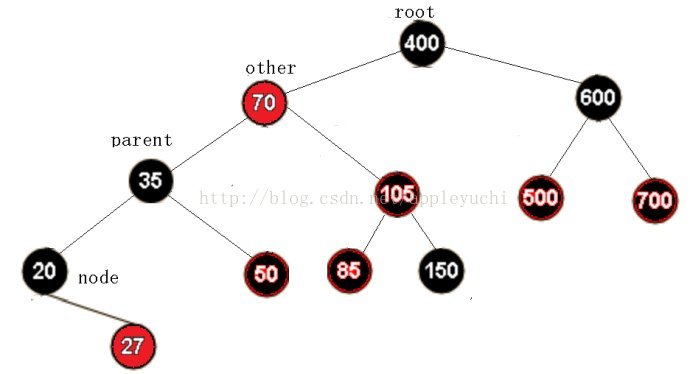
可见上面由情况3变为情况1b进行了1次旋转,情况1b重构进行了两次旋转操作。
红黑树操作的时间代价
红黑树检索、插入、删除操作平均和最差时间都是O(lgn):

红黑树数据结构的构造一般需要包含几个元素:数据域、左指针、右指针、颜色、父指针(从上到下递归进行不需要父指针???)。
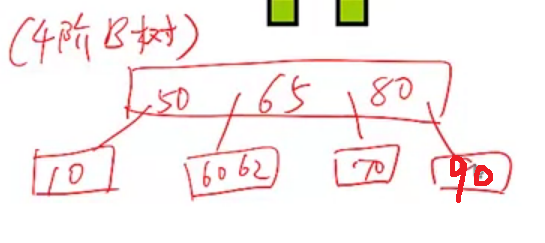
红黑树对应于4阶B树,也称为2-3-4树,两者之间可以相互转换。把红色的节点吸收到父节点,就将红黑树变为了4阶的B树。
红黑树Java实现
关于Java实现,可以参考红黑树(五)之 Java的实现,代码非常简单易懂,和上面讲述的理论知识完全相符,这里就不重复造轮子了。。
(完)