数据结构

数据结构之二叉搜索树

Posted by W-M on February 13, 2017

本篇随笔主要介绍 Java 实现二叉搜索树的查找、插入、删除、遍历等内容。有不对的地方，请指出。

二叉搜索树简介

二叉搜索树需满足以下四个条件：

  1. 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
  2. 若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
  3. 任意节点的左、右子树也分别为二叉查找树；
  4. 没有键值相等的节点。

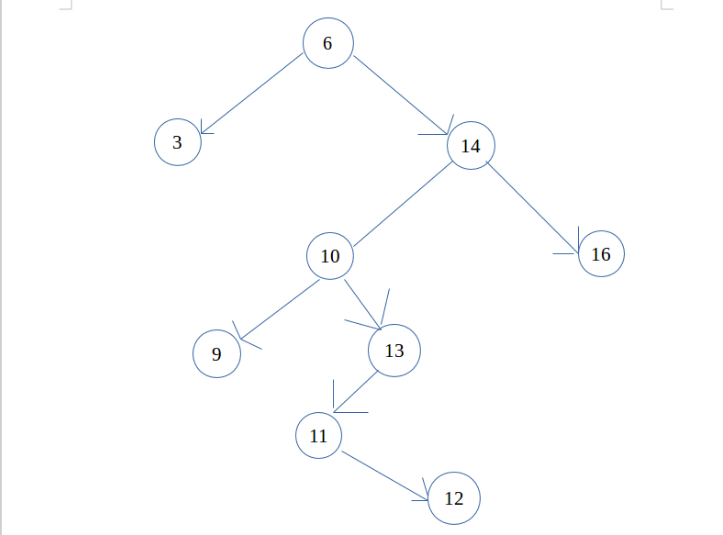
二叉搜索树举例： 二叉搜索树示例

图1：二叉搜索树示例

接下来将基于图一介绍二叉搜索树Java代码实现。

二叉搜索树Java实现

首先，应先有一个节点对象相关的类，命名为 Node。

class Node {
    int key;
    int value;
    Node leftChild;
    Node rightChild;

    public Node(int key, int value) {
        this.key = key;
        this.value = value;
    }

    public void displayNode() {

    }
}

Node 类中包含 key 值，用于确定节点在树中相应位置，value 值代表要存储的内容，还含有指向左右孩子节点的两个引用。

接下来看下搜索树相应的类：

class Tree {
    Node root;//保存树的根

    public Node find(int key) {//查找指定节点
        
    }

    public void insert(int key, int value) {//插入节点
       
    }

    public boolean delete(int key) {//删除指定节点
        
    }

    private Node getDirectPostNode(Node delNode) {//得到待删除节点的直接后继节点
        
    }

    public void preOrder(Node rootNode) {//先序遍历树
       
    }

    public void inOrder(Node rootNode) {//中序遍历树
        
    }

    public void postOrder(Node rootNode) {//后序遍历树
        
    }
}

类中表示树的框架，包含查找、插入、遍历、删除相应方法，其中删除节点操作最为复杂，接下来一一介绍。

查找某个节点

由于二叉搜索树定义上的特殊性，只需根据输入的 key 值从根开始进行比较，若小于根的 key 值，则与根的左子树比较，大于根的key值与根的右子树比较，以此类推，找到则返回相应节点，否则返回 null。

public Node find(int key) {
    Node currentNode = root;
    while (currentNode != null && currentNode.key != key) {
        if (key < currentNode.key) {
            currentNode = currentNode.leftChild;
        } else {
            currentNode = currentNode.rightChild;
        }
    }
    return currentNode;
}

插入节点

与查找操作相似，由于二叉搜索树的特殊性，待插入的节点也需要从根节点开始进行比较，小于根节点则与根节点左子树比较，反之则与右子树比较，直到左子树为空或右子树为空，则插入到相应为空的位置，在比较的过程中要注意保存父节点的信息 及 待插入的位置是父节点的左子树还是右子树，才能插入到正确的位置。

public void insert(int key, int value) {
    if (root == null) {
        root = new Node(key, value);
        return;
    }
    Node currentNode = root;
    Node parentNode = root;
    boolean isLeftChild = true;
    while (currentNode != null) {
        parentNode = currentNode;
        if (key < currentNode.key) {
            currentNode = currentNode.leftChild;
            isLeftChild = true;
        } else {
            currentNode = currentNode.rightChild;
            isLeftChild = false;
        }
    }
    Node newNode = new Node(key, value);
    if (isLeftChild) {
        parentNode.leftChild = newNode;
    } else {
        parentNode.rightChild = newNode;
    }
}

遍历二叉搜索树

遍历操作与遍历普通二叉树操作完全相同，不赘述。

public void preOrder(Node rootNode) {
    if (rootNode != null) {
        System.out.println(rootNode.key + " " + rootNode.value);
        preOrder(rootNode.leftChild);
        preOrder(rootNode.rightChild);
    }
}

public void inOrder(Node rootNode) {
    if (rootNode != null) {
        inOrder(rootNode.leftChild);
        System.out.println(rootNode.key + " " + rootNode.value);
        inOrder(rootNode.rightChild);
    }
}

public void postOrder(Node rootNode) {
    if (rootNode != null) {
        postOrder(rootNode.leftChild);
        postOrder(rootNode.rightChild);
        System.out.println(rootNode.key + " " + rootNode.value);
    }
}

删除指定节点

在二叉搜索树中删除节点操作较复杂，可分为以下三种情况。

1、待删除的节点为叶子节点，可直接删除。

public boolean delete(int key) {
    Node currentNode = root;//用来保存待删除节点
    Node parentNode = root;//用来保存待删除节点的父亲节点
    boolean isLeftChild = true;//用来确定待删除节点是父亲节点的左孩子还是右孩子
    while (currentNode != null && currentNode.key != key) {
        parentNode = currentNode;
        if (key < currentNode.key) {
            currentNode = currentNode.leftChild;
            isLeftChild = true;
        } else {
            currentNode = currentNode.rightChild;
            isLeftChild = false;
        }
    }
    if (currentNode == null) {
        return false;
    }
    if (currentNode.leftChild == null && currentNode.rightChild == null) {//要删除的节点为叶子节点
        if (currentNode == root)
            root = null;
        else if (isLeftChild)
            parentNode.leftChild = null;
        else
            parentNode.rightChild = null;
    } 
    ......

}

2、待删除节点只有一个孩子节点。

例如删除图一中的 key 值为 11 的节点，只需将 key 值为 13 的节点的左孩子指向 key 值为 12的节点即可达到删除 key 值为 11 的节点的目的。

由以上分析可得代码如下（接上述 delete 方法省略号后）：

else if (currentNode.rightChild == null) {//要删除的节点只有左孩子
    if (currentNode == root)
        root = currentNode.leftChild;
    else if (isLeftChild)
        parentNode.leftChild = currentNode.leftChild;
    else
        parentNode.rightChild = currentNode.leftChild;
} else if (currentNode.leftChild == null) {//要删除的节点只有右孩子
    if (currentNode == root)
        root = currentNode.rightChild;
    else if (isLeftChild)
        parentNode.leftChild = currentNode.rightChild;
    else
        parentNode.rightChild = currentNode.rightChild;
} 
   ......

3、待删除节点既有左孩子，又有右孩子。

例如删除图一中 key 值为 10 的节点，这时就需要用 key 值为 10 的节点的中序后继节点（节点 11）来代替 key 值为 10 的节点，并删除 key 值为 10 的节点的中序后继节点，由中序遍历相关规则可知， key 值为 10 的节点的直接中序后继节点一定是其右子树中 key 值最小的节点，所以此中序后继节点一定不含子节点或者只含有一个右孩子，删除此中序后继节点就属于上述 1,2 所述情况。图一中 key 值为 10 的节点的直接中序后继节点 为 11，节点 11 含有一个右孩子 12。

所以删除 图一中 key 值为 10 的节点分为以下几步：

a、找到 key 值为 10 的节点的直接中序后继节点（即其右子树中值最小的节点 11），并删除此直接中序后继节点。

private Node getDirectPostNode(Node delNode) {//方法作用为得到待删除节点的直接后继节点
        
        Node parentNode = delNode;//用来保存待删除节点的直接后继节点的父亲节点
        Node direcrPostNode = delNode;//用来保存待删除节点的直接后继节点
        Node currentNode = delNode.rightChild;
        while (currentNode != null) {
            parentNode = direcrPostNode;
            direcrPostNode = currentNode;
            currentNode = currentNode.leftChild;
        }
        if (direcrPostNode != delNode.rightChild) {//从树中删除此直接后继节点
            parentNode.leftChild = direcrPostNode.rightChild;
            direcrPostNode.rightChild = null;
        }
        return direcrPostNode;//返回此直接后继节点
        
}

b、将此后继节点的 key、value 值赋给待删除节点的 key，value值。(接情况二中省略号代码之后)

else { //要删除的节点既有左孩子又有右孩子

        //思路：用待删除节点右子树中的key值最小节点的值来替代要删除的节点的值,然后删除右子树中key值最小的节点
        //右子树key最小的节点一定不含左子树,所以删除这个key最小的节点一定是属于叶子节点或者只有右子树的节点
        Node directPostNode = getDirectPostNode(currentNode);
        currentNode.key = directPostNode.key;
        currentNode.value = directPostNode.value;

}

至此删除指定节点的操作结束。

最后给出完整代码及简单测试代码及测试结果：

class Node {
    int key;
    int value;
    Node leftChild;
    Node rightChild;

    public Node(int key, int value) {
        this.key = key;
        this.value = value;
    }

    public void displayNode() {

    }
}

class Tree {
    Node root;

    public Node find(int key) {
        Node currentNode = root;
        while (currentNode != null && currentNode.key != key) {
            if (key < currentNode.key) {
                currentNode = currentNode.leftChild;
            } else {
                currentNode = currentNode.rightChild;
            }
        }
        return currentNode;
    }

    public void insert(int key, int value) {
        if (root == null) {
            root = new Node(key, value);
            return;
        }
        Node currentNode = root;
        Node parentNode = root;
        boolean isLeftChild = true;
        while (currentNode != null) {
            parentNode = currentNode;
            if (key < currentNode.key) {
                currentNode = currentNode.leftChild;
                isLeftChild = true;
            } else {
                currentNode = currentNode.rightChild;
                isLeftChild = false;
            }
        }
        Node newNode = new Node(key, value);
        if (isLeftChild) {
            parentNode.leftChild = newNode;
        } else {
            parentNode.rightChild = newNode;
        }
    }

    public boolean delete(int key) {
        Node currentNode = root;
        Node parentNode = root;
        boolean isLeftChild = true;
        while (currentNode != null && currentNode.key != key) {
            parentNode = currentNode;
            if (key < currentNode.key) {
                currentNode = currentNode.leftChild;
                isLeftChild = true;
            } else {
                currentNode = currentNode.rightChild;
                isLeftChild = false;
            }
        }
        if (currentNode == null) {
            return false;
        }
        if (currentNode.leftChild == null && currentNode.rightChild == null) {
            //要删除的节点为叶子节点
            if (currentNode == root)
                root = null;
            else if (isLeftChild)
                parentNode.leftChild = null;
            else
                parentNode.rightChild = null;
        } else if (currentNode.rightChild == null) {//要删除的节点只有左孩子
            if (currentNode == root)
                root = currentNode.leftChild;
            else if (isLeftChild)
                parentNode.leftChild = currentNode.leftChild;
            else
                parentNode.rightChild = currentNode.leftChild;
        } else if (currentNode.leftChild == null) {//要删除的节点只有右孩子
            if (currentNode == root)
                root = currentNode.rightChild;
            else if (isLeftChild)
                parentNode.leftChild = currentNode.rightChild;
            else
                parentNode.rightChild = currentNode.rightChild;
        } else { //要删除的节点既有左孩子又有右孩子
            //思路：用待删除节点右子树中的key值最小节点的值来替代要删除的节点的值,然后删除右子树中key值最小的节点
            //右子树key最小的节点一定不含左子树,所以删除这个key最小的节点一定是属于叶子节点或者只有右子树的节点
            Node directPostNode = getDirectPostNode(currentNode);
            currentNode.key = directPostNode.key;
            currentNode.value = directPostNode.value;
        }
        return true;
    }

    private Node getDirectPostNode(Node delNode) {//方法作用为得到待删除节点的直接后继节点

        Node parentNode = delNode;//用来保存待删除节点的直接后继节点的父亲节点
        Node direcrPostNode = delNode;//用来保存待删除节点的直接后继节点
        Node currentNode = delNode.rightChild;
        while (currentNode != null) {
            parentNode = direcrPostNode;
            direcrPostNode = currentNode;
            currentNode = currentNode.leftChild;
        }
        if (direcrPostNode != delNode.rightChild) {//从树中删除此直接后继节点
            parentNode.leftChild = direcrPostNode.rightChild;
            direcrPostNode.rightChild = null;
        }
        return direcrPostNode;//返回此直接后继节点

    }

    public void preOrder(Node rootNode) {
        if (rootNode != null) {
            System.out.println(rootNode.key + " " + rootNode.value);
            preOrder(rootNode.leftChild);
            preOrder(rootNode.rightChild);
        }
    }

    public void inOrder(Node rootNode) {
        if (rootNode != null) {
            inOrder(rootNode.leftChild);
            System.out.println("key: " + rootNode.key + " " + "value: " + rootNode.value);
            inOrder(rootNode.rightChild);
        }
    }

    public void postOrder(Node rootNode) {
        if (rootNode != null) {
            postOrder(rootNode.leftChild);
            postOrder(rootNode.rightChild);
            System.out.println(rootNode.key + " " + rootNode.value);
        }
    }
　　　　
    　　private void destroy(Node tree) {
     　　    if (tree==null)
     　　        return ;
 
       　　  if (tree.left != null)
      　　       destroy(tree.leftChild);
      　　   if (tree.right != null)
       　　      destroy(tree.rightChild);
 
      　　  tree=null;
  　　  }
　　　　
　　　　public void destory() {
　　　　　　destory(root);
　　　　}
} 
public class BinarySearchTreeApp { 
　 public static void main(String[] args) {
　　　　　 Tree tree = new Tree(); 
　　　 tree.insert(6, 6);//插入操作,构造图一所示的二叉树 
　　　 tree.insert(3, 3); 
　　　　tree.insert(14, 14); 
　　　 tree.insert(16, 16); 
　　　 tree.insert(10, 10); 
　　　 tree.insert(9, 9); 
　　　　tree.insert(13, 13); 
　　　 tree.insert(11, 11); 
　　　　tree.insert(12, 12); 
　　 System.out.println("删除前遍历结果"); 
　　　　tree.inOrder(tree.root);//中序遍历操作 
　　 System.out.println("删除节点10之后遍历结果"); 
　　　　tree.delete(10);//删除操作 
 　　　　tree.inOrder(tree.root); 168  
　} 
}

测试结果： 测试结果

图2：测试结果

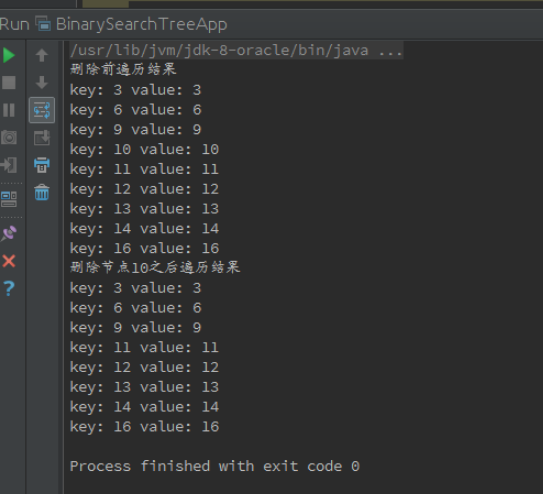
(完)

CATALOG
    FEATURED TAGS
    数据结构 Java基础 JDK源码阅读 Spring Web杂记 操作系统 协议 数据库 并发 消息中间件 产品 算法 MyBatis